Determinantes

 

👫👷            👷👸👨

👩👧           👪💆👪

                   👤😇😔

Determinantes

          Calculamos o determinante de matrizes quadradas, isto é, aquelas em que o número de linhas é igual ao número de colunas. Observe:

          Definimos como determinante da matriz A (det A) o número que é obtido pela operação dos elementos que compõem A.

·Caso A possua uma linha e uma coluna (A_{1 X 1}), então o determinante será representado pelo único elemento que compõe A. Exemplo:

A = (10)
det A = 10

·     Se A possuir duas linhas e colunas (A_{2 x 2}), então o determinante (det A_{2 x 2}) será dado pela diferença entre os produtos da diagonal principal da matriz A pelo produto dos elementos que compõem a sua diagonal secundária. Veja abaixo como é feito o cálculo do determinante de uma matriz 2 por 2 (A _{2 X 2}).

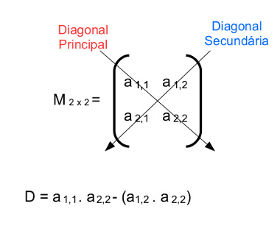
Para toda matriz quadrada 2 por 2, o cálculo do determinante é realizado da forma como está demonstrado acima. Caso a matriz quadrada seja do tipo M _{3 X 3}, M _{4 X 4}, M _{5 X 5} e assim por diante, calculamos o seu determinante executando os passos descritos abaixo:

1.    Faça o espelhamento da primeira e da segunda coluna da matriz, ou seja, repita a primeira e a segunda coluna;

2.    Realize os produtos de cada diagonal principal e secundária separadamente;

3.    Efetue a soma entre os termos obtidos dos produtos de cada diagonal;

4.    Realize a diferença entre os resultados obtidos referente à soma dos termos das diagonais principais e das secundárias. No fim desses cálculos, teremos o determinante da matriz.

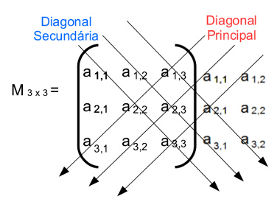
det M_{3 X 3} = a _1,1 . a _2,2 . a _3,3 + a _1,2 + a _1,2 . a _2,3 . a _3,1 + a _1,3 . a _2,1 . a _3,2 - ( a _1,3 . a _2,2 . a _3,1 + a _1,1 . a _2,3 . a _3,2 + a _1,2 . a _2,1 . a _3,3).