Aula do dia 28/04/21 2º Anos E e F do E.M

 Projeção vertical👉Seno do ângulo alfa  projeção do sol 😃 na vertical

Projeção na horizontal cosseno do ângulo alfa com projeção do sol 😃 na horizontal👈

Problemas de contagem EJA

 1) Se temos 6 agasalhos podemos escolher 6 deles na 2.feira, e na 3.feira sobram 5 escolhas, na 4.feira são 4 escolhas, na 5.feira restam 3 escolhas, e na 6.feira restam apenas 2 escolhas, para termos o total de maneiras basta multiplicarmos os números de escolha de cada dia não é mesmo?

2) Se queremos saber o total de escolhas em cada dia, basta dividirmos por 5 (dias de segunda a sexta) ou para ser mais preciso dividir por 6 se considerarmos o dia de sábado e temos as possibilidades de escolhas de cada dia.

Potenciação Recuperação e aprofundamento para os 3ª Termos A,B e C,

 Potenciação

O resultado de uma potenciação é obtido pelo produto de fatores iguais e a sua representação é dada por  aⁿ = a . a . a . a ...

A operação realizada na potenciação é uma multiplicação e é representada da seguinte forma:

Potenciação

aⁿ = a . a . a . a …

a = base
n = expoente
a . a . a . a … = produto de n fatores iguais que gera como resultado a potência

Para compreender melhor, acompanhe os exemplos abaixo:

⇒ 2³ = 2 . 2 . 2 = 8

2 = base
3 = expoente
2 . 2 . 2 = produto de fatores
8 = potência

Como o expoente é 3, tivemos que repetir a base, que é 2 três vezes, em um produto.

⇒ 5⁴ = 5 . 5 . 5 . 5 = 625

5 = base
4 = expoente
5 . 5 . 5 . 5 = produto de fatores
625 = potência

Como o expoente é 4, tivemos que repetir a base, que é 5 quatro vezes, em um produto.

⇒ 10² = 10 . 10 = 100

10 = base
2 = expoente
10 . 10 = produto de fatores
100 = potência

Como o expoente é 2, tivemos que repetir a base, que é 10 duas vezes, em um produto.

Tipos de potenciação

·         Base real e expoente inteiro

Quando o expoente é inteiro, significa que ele pode possuir número negativo ou positivo.

⇒ Expoente positivo: Quando a base for um número real e o expoente for positivo, obteremos a potência efetuando o produto dos fatores. Acompanhe alguns exemplos:

2⁺² = 2 . 2 = 4
0,3⁺³ = 0,3 . 0,3 . 0,3 = 0,027
(½ )⁺² = ½ . ½ = ¼

⇒ Expoente negativo: Se o expoente é negativo, devemos fazer o inverso do número que é trocar numerador com denominador, para o expoente passar a ser positivo. Observe alguns exemplos:

2^-2 =   1  = 1 . 1 = 1
        2⁺²     2   2    4

Não pare agora... Tem mais depois da publicidade ;)

0,3 ^{– 3} = (3)^-3 = (10)⁺³ = 10 . 10 . 10 = 1000 = 37,037
           (10)^-3     (3)⁺³        3 . 3 . 3        27

(½ )^-2 = (2/1)⁺² = 2 . 2 = 4

⇒ Expoente igual a 1

Quando o expoente for igual a um positivo, a potência será o próprio número da base. Veja os exemplos abaixo:

a¹ = a
2¹ = 2
4¹ = 4
100¹ = 100

⇒ Expoente igual a 0

Se o expoente for 0, a reposta referente à potência sempre será 1. Acompanhe os exemplos:

a⁰ = 1
1000⁰ = 1
25⁰ = 1

Propriedades da potenciação

As propriedades da potenciação são utilizadas para simplificar os cálculos. Há, no total, cinco propriedades:

1.    Produto de potências de mesma base: conserva a base e soma os expoentes. Exemplos:

aⁿ . a^m = a^{n + m}
2² . 2³ = 2^{2 + 3} = 2⁵
4⁵ . 4² = 4^{5 + 2} = 4⁷

2.    Divisão de potências de mesma base: conserva a base e subtrai os expoentes. Exemplos:

aⁿ : a^m = aⁿ = a^{n - m}
              a^m
5⁶ : 5² = 5⁶ = 5^{6 – 2} = 5⁴
             5²
9² : 9³ = 9² = 9^{2 – 3} = 9^-1
             9³

3.    Potência de potência: devemos multiplicar os expoentes. Exemplos:

(aⁿ)^m = a^{n . m}
(7⁴)² = 7^{4 . 2} = 7⁸
(12³)² = 12^{3 . 2} = 12⁶

4.    Potência de um produto: o expoente geral é expoente dos fatores. Exemplos:

(a . b)ⁿ = ( aⁿ . bⁿ)
(4 . 5)² = (4² . 5²)
(12 . 9)³ = (12³ . 9³)

5.    Multiplicação de potências com o mesmo expoente: conserva o expoente e multiplica as bases. Exemplo:

aⁿ . bⁿ = (a . b)ⁿ
4² . 6² = (4 . 6)²
7³ . 4³ = (7 . 4)³

Os elementos da potenciação são: base, expoente e potência

 

 

Conceitos Geométricos 3º Termos.

 

     A Geometria Analítica estabelece conexões entre geometria e álgebra, de modo que os conceitos da geometria são analisados por meio de processos algébricos. Ela foi criada pelo matemático francês René Descartes e, por isso, também é chamada de geometria cartesiana. Vide aula: Coordenadas cartesianas ou acompanhe até o final desta postagem.

     Todos os objetos, figuras e relações já obtidas na geometria euclidiana clássica (geometria plana e espacial) são estudados na geometria analítica por meio da álgebra. Isso expande os conceitos da geometria, que agora podem ser analisados de um modo completamente novo, e introduz conceitos que ainda não podiam ser considerados ou que não podiam ser explorados ao máximo na geometria euclidiana. Um exemplo disso é o conceito de distância entre um ponto e uma reta.

As bases da Geometria Analítica

A base da geometria analítica está em representar os pontos de uma reta utilizando os números reais. Cada ponto de uma reta é representado por (ou representa) um único número real. Esse número real é obtido pela distância entre o referido ponto e a origem da reta, que é o ponto relacionado com o número zero.

O conceito de distância, portanto, é um dos mais importantes dentro da Geometria Analítica. Por meio dele são definidos outros conceitos importantes, como os de círculo e circunferência. Além disso, a maioria das definições algébricas de figuras geométricas é obtida por intermédio do conceito de distância.

Exemplo de representação do ponto de uma reta por um número real

Posteriormente, essa ideia foi expandida para a representação de pontos no plano, de modo que cada ponto do plano é representado por um único par de números reais conhecido como par ordenado. A imagem abaixo ilustra como o par ordenado (2,1) representa o ponto A.

Exemplo da representação de um ponto no plano por um par de números reais

Já os pontos do espaço são representados por um conjunto de três números reais,

conhecidos como ternos ordenados. Cada terno ordenado representa apenas um único ponto no espaço.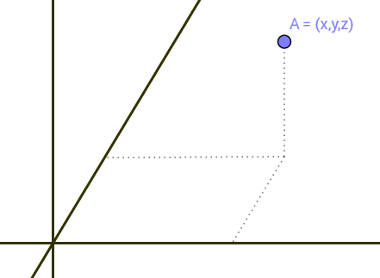

Se um ponto pertence a uma reta e é representado por um número real, dizemos que o espaço onde esse ponto está localizado (a reta) possui apenas uma dimensão e o número real é chamado de coordenada do ponto.

Caso o ponto pertença a um plano, é representado por um par de números reais. O espaço onde está localizado (o plano) possui duas dimensões e esse ponto possui duas coordenadas.

Desse modo, o número de coordenadas que um ponto possui é igual ao número de dimensões que possui o espaço onde esse ponto está localizado. O ponto pertencente ao espaço tridimensional, por exemplo, possuirá três dimensões e será representado por três coordenadas. A figura acima retrata o ponto A, que pertence ao espaço tridimensional e é representado pelo terno ordenado (x,y,z).

O que a Geometria Analítica estuda?

Qualquer objeto matemático, figura geométrica, forma, etc., que esteja no espaço pode ser representado geometricamente por um desenho ou algebricamente por uma fórmula matemática. Essa fórmula é o que materializa a Geometria Analítica e conecta a geometria à álgebra.

O estudo de Geometria Analítica geralmente é dividido nos seguintes tópicos: Estudo Analítico do Ponto

1 – O que é ponto e localização?

2 – Plano Cartesiano

3 – Distância entre dois pontos

4 – Conjuntos de pontos

Estudo Analítico da Reta

1 – Equação geral da reta

2 – Posições relativas entre retas

3 – Ângulo entre retas

4 – Paralelismo

5 – Perpendicularidade

6 – Distância entre ponto e reta

Estudo analítico da circunferência

1 – Equação da circunferência

2 – Posição relativa entre ponto e circunferência

3 – Posição relativa entre reta e circunferência

4 – Posição relativa entre circunferência e circunferência

Vetores

1 – O que são e representação de vetores

2 – Operações básicas envolvendo vetores

3 – Ângulo entre vetores

Cônicas

1 – Elipse

2 – Hipérbole

3 – Parábola

Algumas relações entre figuras geométricas e fórmulas algébricas

Coordenadas cartesianas e o caça palavras

As palavras deste caça palavras estão escondidas na horizontal, vertical e diagonal, sem palavras ao contrário.

• BOMBA
• CÚSPIDES
• ELÁSTICA
• FOLHETOS
• MEIA
• MUSCULAR
• PERNAS
• SAFENA
• SISTEMA
• VEIAS
• VENOSAS
• VÁLVULAS

• 
  

E	I	E	C	Ú	S	P	I	D	E	S	F
L	L	O	P	S	E	S	👇O	H	R	G	O
Á	S	H	H	N	I	D	T	J	E	O	L
S	👇N	M	U	S	C	U	L	👇A	R	H	H
T	H	V	T	P	E	R	N	A	S	V	E
I	R	E	P	N	M	T	T	O	Á	E	T
C	M	N	N	A	👇S	C	B	L	H	I	O
A	R	O	Y	M	T	J	V	C	U	A	S
M	E	S	👇G	E	A	U	A	O	👇U	S	H
C	S	A	E	I	L	C	B	O	M	B	A
Y	S	S	E	A	P	H	T	E	O	T	M
A	H	P	S	I	S	A	F	E	N	A	A

                                     

                                 eixo x horizontal e eixo y vertical

                                                                            👇

            Observe que  a origem do sistema é S(0,0) 

Exemplos: As localizações da letra A azul é (3,3) ou seja 3 letras a direita de S (origem de nosso sistema) e 3 letras acima de S,

e da letra U lilás é (4,-3) ou seja 4 letras a direita de S e 3 letras abaixo de S.

Atividades: Observar o caça palavras e as ordem das letras coloridas buscar a localização das mesmas em relação a origem  S(0,0) do sistema de coordenadas.

Forneça as coordenadas das letras coloridas segundo os exemplos acima,  observando que quando abaixo ou a esquerda da origem coloca-se um sinal de negativo na frente do número.

a) Coordenadas da letra O

b) Coordenadas da letra N

c) Coordenadas da letra G

• 
  

Dicas para resolver rapidamente questões de concursos

      Questões que envolvem duas idades e quem é o mais velho.

Fábio é 6 anos mais velho que Marcelo e a soma das idades entre eles é 42 anos.

total da idade deles é 42 anos, é só dividir 42 por 2, e literalmente é a idade dividida para cada um deles vai ser 21 anos, e note que o mais velho tem 6 anos a mais, então basta fazer,

6 divido também por dois e obtemos 3, basta colocarmos 3 a mais para o mais velho que é Marcelo e tirar 3 anos de fábio, assim teremos:

21 anos + 3 anos = 24 anos que é a Idade de Marcelo e 21 anos -3 anos = 18 anos que é idade de Fábio.

Na outra aula daremos mais dicas para facilitar as resoluções de questões matemáticas.

É fácil resolver Razão entre dois números.

                     Razão é de 7/6  entre dois números em que o maior deles é 42 e o menor deles é x.

basta termos a constante proporcional K, temos que como o 7 é o  maior, fazemos 7.K= 42 por ser o maior entre os dois números 42 e x, e resolvemos a equação K=42/7=6 e agora temos a outra expressão que envolve o menor número da razão 7 e 6, temos a seguinte expressão 6.k = 6.6 =36 qe é o menor número. 42: 7 = 6 e 6.6=36

outro exemplo é a razão entre a minha idade e do meu tio é 2/5 e as duas idades juntas é 56.Qual é a minha idade e qual é a idade do meu tio?

sempre quando tem o total podemos fazer este raciocínio, 2k + K5= 56 , 7k=56 k=8 

Portanto temos que E/T=2k/3k

 como o k=8 temos que 2.8=16 anos minha idade e do meu tio é 40 anos ou seja 5.8=40 anos.

outro exemplo é total é de 20 kg de carne ao dividir na razão de 2/3 temos que 2k+3k=20 ou seja temos que 5k=20 logo k=4 pois estamos na tabuada do 5.

logo o maior pedaço é 3k= 3.4 = 12 kg que é o maior pedaço.

Dicas fáceis e rápidas para resolver regra de três compostas.

 Para se resolver regra de três compostas de maneira mais fácil e prática.

Dica: Qual é o objetivo do problema? No caso abaixo o objetivo é construir uma casa com operários, certo?

ou seja construir uma casa 

sabendo-se que 3 operários fazem uma casa em 10 dias, trabalhando 8 horas ao dia. 

Quantos dias farão uma outra casa nas mesmas condições da anterior, se forem 6 trabalhadores trabalhando 10 horas ao dia?

coloque as grandezas na ordem apresentada:

Operários                   dias                    horas/dia

3             troque👉     10                           8

6                                   x   👈  por           10

A nova configuração fica assim:

Operários                  dias                        horas/dia

3                                 10         troquei👉   10

6                                  x                              8 👈  por

Agora é só multiplicar os numeradores e igualar  👉ao multiplicar também os denominadores,

3/6                             10/x         =    10/8

3.10.10 =👉  6.x.8

300 = 48x

x=300:48      ou seja x= 6,25 ou ainda 6 horas e 15minutos.