Conceitos Geométricos 3º Termos.

 

     A Geometria Analítica estabelece conexões entre geometria e álgebra, de modo que os conceitos da geometria são analisados por meio de processos algébricos. Ela foi criada pelo matemático francês René Descartes e, por isso, também é chamada de geometria cartesiana. Vide aula: Coordenadas cartesianas ou acompanhe até o final desta postagem.

     Todos os objetos, figuras e relações já obtidas na geometria euclidiana clássica (geometria plana e espacial) são estudados na geometria analítica por meio da álgebra. Isso expande os conceitos da geometria, que agora podem ser analisados de um modo completamente novo, e introduz conceitos que ainda não podiam ser considerados ou que não podiam ser explorados ao máximo na geometria euclidiana. Um exemplo disso é o conceito de distância entre um ponto e uma reta.

As bases da Geometria Analítica

A base da geometria analítica está em representar os pontos de uma reta utilizando os números reais. Cada ponto de uma reta é representado por (ou representa) um único número real. Esse número real é obtido pela distância entre o referido ponto e a origem da reta, que é o ponto relacionado com o número zero.

O conceito de distância, portanto, é um dos mais importantes dentro da Geometria Analítica. Por meio dele são definidos outros conceitos importantes, como os de círculo e circunferência. Além disso, a maioria das definições algébricas de figuras geométricas é obtida por intermédio do conceito de distância.

Exemplo de representação do ponto de uma reta por um número real

Posteriormente, essa ideia foi expandida para a representação de pontos no plano, de modo que cada ponto do plano é representado por um único par de números reais conhecido como par ordenado. A imagem abaixo ilustra como o par ordenado (2,1) representa o ponto A.

Exemplo da representação de um ponto no plano por um par de números reais

Já os pontos do espaço são representados por um conjunto de três números reais,

conhecidos como ternos ordenados. Cada terno ordenado representa apenas um único ponto no espaço.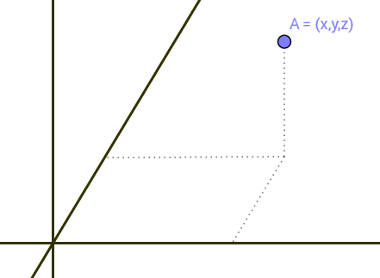

Se um ponto pertence a uma reta e é representado por um número real, dizemos que o espaço onde esse ponto está localizado (a reta) possui apenas uma dimensão e o número real é chamado de coordenada do ponto.

Caso o ponto pertença a um plano, é representado por um par de números reais. O espaço onde está localizado (o plano) possui duas dimensões e esse ponto possui duas coordenadas.

Desse modo, o número de coordenadas que um ponto possui é igual ao número de dimensões que possui o espaço onde esse ponto está localizado. O ponto pertencente ao espaço tridimensional, por exemplo, possuirá três dimensões e será representado por três coordenadas. A figura acima retrata o ponto A, que pertence ao espaço tridimensional e é representado pelo terno ordenado (x,y,z).

O que a Geometria Analítica estuda?

Qualquer objeto matemático, figura geométrica, forma, etc., que esteja no espaço pode ser representado geometricamente por um desenho ou algebricamente por uma fórmula matemática. Essa fórmula é o que materializa a Geometria Analítica e conecta a geometria à álgebra.

O estudo de Geometria Analítica geralmente é dividido nos seguintes tópicos: Estudo Analítico do Ponto

1 – O que é ponto e localização?

2 – Plano Cartesiano

3 – Distância entre dois pontos

4 – Conjuntos de pontos

Estudo Analítico da Reta

1 – Equação geral da reta

2 – Posições relativas entre retas

3 – Ângulo entre retas

4 – Paralelismo

5 – Perpendicularidade

6 – Distância entre ponto e reta

Estudo analítico da circunferência

1 – Equação da circunferência

2 – Posição relativa entre ponto e circunferência

3 – Posição relativa entre reta e circunferência

4 – Posição relativa entre circunferência e circunferência

Vetores

1 – O que são e representação de vetores

2 – Operações básicas envolvendo vetores

3 – Ângulo entre vetores

Cônicas

1 – Elipse

2 – Hipérbole

3 – Parábola

Algumas relações entre figuras geométricas e fórmulas algébricas

Coordenadas cartesianas e o caça palavras

As palavras deste caça palavras estão escondidas na horizontal, vertical e diagonal, sem palavras ao contrário.

• BOMBA
• CÚSPIDES
• ELÁSTICA
• FOLHETOS
• MEIA
• MUSCULAR
• PERNAS
• SAFENA
• SISTEMA
• VEIAS
• VENOSAS
• VÁLVULAS

• 
  

E	I	E	C	Ú	S	P	I	D	E	S	F
L	L	O	P	S	E	S	👇O	H	R	G	O
Á	S	H	H	N	I	D	T	J	E	O	L
S	👇N	M	U	S	C	U	L	👇A	R	H	H
T	H	V	T	P	E	R	N	A	S	V	E
I	R	E	P	N	M	T	T	O	Á	E	T
C	M	N	N	A	👇S	C	B	L	H	I	O
A	R	O	Y	M	T	J	V	C	U	A	S
M	E	S	👇G	E	A	U	A	O	👇U	S	H
C	S	A	E	I	L	C	B	O	M	B	A
Y	S	S	E	A	P	H	T	E	O	T	M
A	H	P	S	I	S	A	F	E	N	A	A

                                     

                                 eixo x horizontal e eixo y vertical

                                                                            👇

            Observe que  a origem do sistema é S(0,0) 

Exemplos: As localizações da letra A azul é (3,3) ou seja 3 letras a direita de S (origem de nosso sistema) e 3 letras acima de S,

e da letra U lilás é (4,-3) ou seja 4 letras a direita de S e 3 letras abaixo de S.

Atividades: Observar o caça palavras e as ordem das letras coloridas buscar a localização das mesmas em relação a origem  S(0,0) do sistema de coordenadas.

Forneça as coordenadas das letras coloridas segundo os exemplos acima,  observando que quando abaixo ou a esquerda da origem coloca-se um sinal de negativo na frente do número.

a) Coordenadas da letra O

b) Coordenadas da letra N

c) Coordenadas da letra G

•